BQ #7: Unit V Derivatives and the Area Problem

Explain in detail where the formula for the difference quotient comes from now that you know! Include all appropriate terminology (secant line, tangent line, h/delta x, etc.) 


 For starters the difference quotient is crucial in calculus since it is like a part of the semester and it is also known as the derivative. The derivative is the slope of all tangent lines on the graph. When using it, we can determine the possible slopes on various graphs. Secant lines are lines that will touch the graph twice but tangent lines are lines that will touch the graph at only one point. H and delta x are variables for the derivative and on a graph, y-value is your f(x) and the x-value is your h or delta x. For derivatives, the thing to add on is that we aren't only finding the difference quotient but we're also determining h as it approaches 0. From here we can do various things like find the tangent slope or the tangent line or any specific values. The thing to remember the the difference quotient is f(x) but the derivative is f'(x) (f prime of x). 

Source 
Derivative
Difference Quotient
Secant & Tangent

BQ #6 Unit U - Introduction to Limits

What is a continuity? What is a discontinuity?

Well for starters, a continuity is when the function is predictable (meaning you know where it's going), no jumps, breaks, or holes (essentially the non-removable discontinuities that we will discuss later on), and can be drawn without lifting your hand up. A discontinuity is divided into two families: removable discontinuities and non-removable discontinuities. The removable discontinuities consist of a point discontinuity. The point discontinuity is where a hole exist and it is also where the limit can also exist at the hole. As for the non-removable discontinuities, they consist of jump discontinuity which is a results from different left/right behaviors, oscillating behavior (which is a wiggly line where there is no real value), and the infinite discontinuity which has a vertical asymptote that results in unbounded behavior. A non-removable discontinuity is where the limit does not exist and the removable discontinuity is where the limit does exist.

What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is simply the intended height of the function and it exist at removable discontinuities that are also known as point discontinuities. The limit does not exist at non-removable discontinuities that are also known as jump, oscillating, and infinite discontinuities. Limits do not exist at non-removable discontinuities because of different left right behavior where the lines do not meet together at one point, or when there is no real value in the oscillating discontinuity where it does not approach a single value, or when the line reaches towards infinity because infinity is not defined as a real number. Limits do not also exist at the infinite discontinuity because of the vertical asymptotes that result in unbounded behavior.
The main difference between a limit and a value is that the limit is the intended height of the function while the graph is the actual height of the function.

How do we evaluate limits numerically, graphically, and algebraically, (VANG)?

Algebraically

By using direct substitution, factoring/dividing, or the conjugate method, we can solve for these limits algebraically. For direct substitution, it is simply plugging in whatever x approaches into the function. However, there are occasions where the result is an indeterminate form which is 0/0. To resolve this problem, we use the factoring/dividing method which removes the hole that causes the indeterminate form. Basically,  the factoring/dividing method is where we will factor out the function as best as we can and then divide/cancel out any like terms to get rid of the hole. As for the conjugate form, this is when there is a radical and we use the conjugate method to make our lives easier and get rid of the radical. However, it is important to remember that we should always use direct substitution method first.

Numerically

For finding limits numerically, we use a table. Usually, we will plug the function into the graphing calculator and hit trace to where the limit supposedly is. Since we can't actually reach the limit, we approximate as close as we can. For example the we can't reach the number 2 but we can get really really close to it so we write it as 1.9, 1.99, 1.999 or 2.1, 2.01, 2.001

Graphically

Graphically is probably the simplest method. To do this we basically just put our fingers on the graph to the left and right of where the limit is. From there we move our fingers closer to the limit. If our fingers touch then that means that we a limit> However, if our fingers do not touch for whatever reason, then that means we do not have a limit so we write DNE (does not exist).


Reference Unit U SSS - Online (Kirch's)

BQ#4 - Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" tangent graph downhill? Use unit circle ratios to explain.

To start off, the ratio for tangent is sine/cosine. So whenever cosine equals 0, we have an asymptote because anything with a denominator of 0 is undefined which is where asymptotes come from. Therefore, the asymptotes for tangent are pi/2 and 3pi/2 which is also at (0,1) and (0,-1). From here, looking at the unit circle, it says that tangent is only positive in the first and third quadrant and negative in the second and fourth quadrant. Therefore, when we graph tangent with its asymptotes, the only possible way to draw tangent and follow its rules is with an uphill line. For cotangent, the ratio is cosine/sine, so whenever sine is equal to 0, there will be an asymptote which is 0 and pi. On the unit circle the asymptotes would be (1,0) and (-1,0). Also on the unit circle, cotangent is only positive on the first and third quadrant. So when plotting the cotangent on the trig graph with its asymptotes, it can only be in an downhill line within its period because of the rules it has to follow.

BQ#3 - Unit T Concept 1-3

How do the graph of sine and cosine relate to each other? 

Tangent 

The ratio for tangent is sine/cosine. From this, we can determine how the graph will look based on if sine/cosine is positive or negative in the quadrants I-IV. Therefore that is why the order for tangent is +_+_ on the unit circle. Another thing is that there are asymptotes in tangent which means that there basically where tangent can't exist because of the undefined trig ratio. With the asymptotes in tangent (an example of the asymptotes are pi/2 and 3pi/2) and the order of positive and negative, it results in the shape of the line which is a uphill line. The uphill line comes from quadrant II with the start being in the negative region because of cosine and then going to positive in quadrant III also because of cosine. 

Cotangent 

The ratio for cotangent is cosine/sine. It is essentially like tangent but its relationship is inverse. For starters, the asymptotes are 0 and pi. This is when sine = 0. The order is once again +_+_ but with the asymptotes in place, the graph will change and it will result in a downhill graph because in Quadrant I, cotangent will be positive but moving to Quadrant II, cotangent will become negative and since the asymptotes restrict the graph from continuing forever, our period shows us a downhill graph. 

Secant 

The ratio for secant is r/x. Since secant is the inverse of cosine, if cosine is positive or negative, secant will also be positive or negative. Going on with asymptotes, since secant is 1/cosine, it is similar to tangent which is sine/cosine meaning that secant will have the same asymptotes as tangent which are pi/2 and 3pi/2. Therefore, when drawing it out, the graph will look similar to the sine/cosine graph but the thing to notice is that the secant graph has almost parabola looking graph. 

Cosecant

The Ratio for cosecant is r/y. Since cosecant is the inverse of sine, this means that where sine is positive or negative on the unit circle also goes along with cosecant. The asymptoes for cosecant also go along with cotangent because the denominator for cosecant and cotangent are sine so the asymptotes are 0 and pi. Once again, the graph will look similar to cos/sine except for the asymptotes which cut off the graph and also the parabolas that are within the periods. 

BQ#5 - Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

Sine and cosine do not have asymptotes because their ratios are y/r and x/r. Relating to the unit circle, r is a constant that always equals one. For there to be an asymptote, the trig ratio should result in a undefined but since r is always equal to one in the unit circle, that means that sine and cosine can't have asymptotes since its trig ratio never results in undefined. As for the four other trig graphs, there are asymptotes because for cosecant and secant, r is not a denominator so the possibility of having an undefined makes it possible for there to be a asymptote. For tangent and cotangent, there is no r, it's just y/x or x/y so having a denominator of 0 is possible so a undefined solution can result in asymptotes in the graphing. Therefore, only sine and cosine do not have asymptotes while the other four trig graphs do.

BQ#2 - Unit T Concept Intro

How do the trig graphs relate to the unit circle?

Trig graphs relate to the unit circle due to trig graphs are just unit circles that are unwrapped. Therefore, each section of the trig graph comes from the quadrants on the unit circle and this results in the distinct pattern of sin/cos/sec/csc/tan/cot on the trig graph. 

Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

A period is one time a trig function goes through its cycle on the cyclical graph. The period for sine and cosine are 2pi because the trigonometric graph is just the unit circle unraveled and for sin and cosine to make the full rotation it takes 2pi. The pattern for sine is +,-,-,+ and the this whole pattern has to occur first for it to be counted as a period. For tangent and cotangent, the period is pi simply because that is the distance for each period. The pattern is only +,-,+,- for tan and since the pattern repeats itself twice in the unit circle, the period would only be half of 2pi which is just pi.

Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

Amplitude is 1/2 the distance between the highest and lowest points on the graph. They are found by looking at the value of a. Sine and cosine have amplitudes because they are the only trig functions that have restrictions. Sin has the ratio y/r and cos has the ratio x/r. Since R is a constant and in the unit circle it equals 1. Therefore the largest and smallest values can only be 1 and -1. Since sin and cosine have these restrictions while the other trig functions do not have this restriction. Therefore, sin and cos have amplitudes but the other functions do not have amplitudes. 

Reflection #1 - Unit Q: Verifying Trig Identities

1. When they ask to verify a trig identity, it means to use your knowledge of trig identities to see if your answer matches with the given answer. Since identities are always true, verifying a trig identity means to prove that the identity is always true. Doing this helps prove the statement that identities are proven facts and formulas that are always true. 

2. Some tips and tricks that I found very helpful for concept 1 and 5 were to always keep the trig functions as simple as you can when solving them. When it's verifying and there are sin/cos mixed in with tan/csc/sec/cot, then it most likely means that you have to use the identities to verify the identity. Also, remember to pay attention to things like if the denominator is a binomial or monomial, any GCF, or when you can multiply by a conjugate and always look for opportunities to use trig identities. 

3. First thing to do is to look at right hand side to see what you are trying to prove and compare to the left hand side. If you see many different trig functions, then that means that identities are going to be used on this problem. From then, go to the left hand side and look at whether it is a binomial or monomial. Also look for any GCF that can be taken out to simplify your problem. From there it is just a matter of trying to get your problem to look like the given. 

Unit Q - Concept 2 - Finding All Trig Functions with Given & Identities

This SP was made in collaboration with Derik Vieyra. Please visit the other awesome posts on their blog by going here. 

Things to notice when going through the Pythagorean/Ratio/Reciprocal identities and with right triangles is that these both result in the same answers even though the methods aren't exactly the same thing. In the end both methods are used to find the ratio for their corresponding trig functions and so that is the relationship between Unit Q Concept 2 and Unit O Concept 5. It is also important to note that where the triangle lies in the quadrant determines which trig functions are positive or negative and that so always be sure to check the quadrants. Once again, thanks for checking out Derik Vierya and my blog!

I/D 3 Unit Q - Concept 1 Pythagorean Identities

Inquiry Activity Summary

1. An identity is proven facts and formulas that are always true. The Pythagorean Theorem is an identity because it is a proven fact and formula that is always true. When presented with the variables x,y, and r, the Pythagorean Theorem is x^2+y^2=r^2. For example, when you want r to =1 then you would use the Pythagorean theorem (x/r)^2 + (y/r)^2 = 1. The ratio for cosine is (x/y) like what you saw in the Pythagorean theorem above and the ratio for sine is (y/r) like the one from above. With this you notice that the sin and cos ratios equal to 1 and there is a relationship between the Pythagorean theorem and the ratio for trig functions. From this we can conclude that cos^2theta + sin^2theta = 1 This is a Pythagorean identity because it is just a rearrangement of the Pythagorean theorem with trig functions that always works. The example below shows how this identity is true. 

2. Our first Pythagorean identity has secant and tangent. To get our other two Pythagorean identities, we have to divide by either cosine or sine because they are basically the golden ratios that give us the rest of the trig functions and are the easiest to deal with. Basically, with sin or cosine, you can form a trig function from them to make cosecant, secant, tangent, and cotangent. With the 2 examples below, this shows us that our pythagorean identity is truly an identity. 

Inquiry Activity Reflection 
1. "The connections that I see between Units N, O, P, and Q so far are.." trig functions being used for explaining almost every concept and the unit circle being referenced back to as well to explain the triangles and the uses. 

2. " If i had to describe trigonometry in THREE words, they would be..." Too many trigs. 

WPP#13 & 14: Unit P Concept 6-7: Applications with Law of Sines & Cosines

Please see my WPP13-14, made in collaboration with Derik Vieyra, by visiting their blog here. Also be sure to check out the other awesome posts on their blog. 

BQ# 1 Unit P Concept 1 & 4 Law of Sines Derivation and Area of an Oblique Triangle

1. Law of Sines - Law of Sines is important because life isn't so perfect that it will always give right triangles. Normal trig functions that we use for special right triangles don't apply to non-right triangles. Therefore we use the law of Sines to solve non-right triangles. Essentially, what we do is set a perpendicular from angle B to create two right triangles and label the line as H. From here we can determine the relationships and use the transitive property
c Sin A = a Sin C to solve for what is needed. From this, we can solve for any side or angle depending on it opposite angle or side. This video below will help you fully understand the concept of Law of Sines.

 

4. Area Formulas - Sometimes you might not be able to get the value of H from the law of Sines. Not to fear because the area of an oblique triangle is very similar to the area of a triangle (A=1/2bh) but since we don't know H, we use (A=1/2b(asinc). This will help us find the value of H so we can use either law of sines or cosines to determine the rest of the triangle if needed. Remember, "The area of an oblique (all sides different lengths!) triangle is one half of the product of two sides and the sine of their included angle." This video below will help you understand this situation better.




Sources
Law of Sines Deriviation
Area of an Oblique Triangle Deriviation

Unit O - WPP 12- Trig Functions with Elevation and Depression

Create your own Playlist on LessonPaths!

Things to look out for when doing problems like these is to remember what you are looking for. Like any other concept in this SSS packet, we have to remember which of the trig functions we are using in order to be able to get the correct answer to our problem. Remember to make sure that your answer is a reasonable answer and not some absurd number. Thanks for looking at my post!

I/D2: Unit O - Derive the SRTs

Inquiry Activity Summary 



 1. To start off, we are given an equilateral triangle with a side length of 1 and are asked to derive a 30-60-90 triangle from it. Following the image above, we first cut a straight line down from the center of the equilateral triangle. Since equilateral triangles are 60* on each corner, the line cut results in a 30* at the very top, 90* at the bottom of the cut line, and a 60* at either the left or right corner since it is left untouched to form a 30* special right triangle. . The height is derived from using the Pythagorean formula (a^2+b^2=c^2) and the image above shows how it is done. Since our answer from the Pythagorean results in fractions, we want to make the answer easier to remember so we multiply by 2 to each side length to result in √3 for 60*, n for 30*, and 2n for the 90*. Since the original side lengths are 1, we can infer that we only have to substitute different values and we should result in the same ratio as the original side lengths of 1 triangle. This is where we substitute in a variable like (n) to represent a value that can be used. 

  2. Next, we are given a square with the side lengths and asked for a 45-45-90 triangle. To do this, we simply cut the square in half with a diagonal line. We do this because each corner of the square is 90* and if we were to cut a side in half, it would result in a 45* so that is where we get our special right triangle. To get our hypotenuse, we simply use the Pythagorean formula like above and after plugging everything we can, our C (hypotenuse) ends up as with the ratio as 1 for the 45* and √2 for our 90*. Since the side lengths are 1, we can infer that using different side lengths will still result in the same ratio so we just add an (n) to substitute as our new value so our ratio becomes n,n,n√2.

Inquiry Activity Reflection 

1. "Something I never noticed before about special right triangles is.." there is actually a ratio that we can use to solve for the sides rather than just memorizing something like a unit circle and its value. 

2.  being "Being able to derive these patterns myself aids in my learning because.."able to understand these concepts is much better for me and my test grade than just barely getting the gist of it. 

I/D Unit N Concept 7 Unit Circle How do SRT and UC Relate?

Inquiry Activity Summary

1. 30* Triangle - This is the smallest angle that is opposite to the smallest side. The 30* angle can be rewritten as radians and is π/6. To convert the * to radians, you use a conversion shown as 30 x π/18. The coordinates for this on a plane are (√3/2,1/2) in quadrant I when plotting the Unit Circle. The unit circle is essentially a circle with the radius of 1. The reference angle is how far an angle is from the x intercept. For 30* angles and its coterminals(angles with the same reference angle), the reference angle is 30*.  

2. 45* Triangle - This is one of the special right triangles (isosceles) that has two sides that are the same angle (45*) and a 90* angle. For converting to radians, 45* x π/180 that results with π/4 in quadrant 1. The sides are in a ratio of 1:1: √2 In a unit circle, the coordinates would be ( √2/2, √2/2) in quadrant I. As for the reference angle, it would be 45* Angles with the same reference angle are 135*, 225*, & 345* that are within 1 revolution. 

3. 60* Triangle - The 60* triangle is part of the 30* triangle to make up the special 30/60/90 right triangle. The 60* angle is the largest angle between the 30/45/60*. In radians, 60* x π/180 = π/3 in quadrant 1. The ordered pair for a 60* angle is (1/2,√3/2) which is the inverse of the 30 ordered pair in quadrant I. The reference angle for a 60* triangle is 60*. For angles that have a reference degree of 60*, the angles are: 60*, 120*, 240*, 300* These angles are within the 1 revolution of a unit circle. 

4. This activity helps me derive the Unit Circle because the first quadrant is comprised of these angles and knowing these angles helps me figure out the rest of the quadrants in the unit circle. There are certain patterns like how much π increases each time or how the reference angles work in a way to make sense and the (+-) for coordinates are supposed to look like. By knowing the special properties of the 3 degrees and its radians, I am able to completely fill out the rest of the unit circle in under 5 minutes without any problems except for the occasional (+-) for the coordinates. 

\











5. All of the angles mentioned above lie in the first quadrant of the unit circle. These values change by degrees, radians, and ordered pairs when drawn in different quadrants because of the special properties of the circles. Notice the 150* in quadrant 2, even though the reference angle may be the same as the 30* in the first quadrant, the new angle and its radians are completely different from the original 30*. Its ordered pairs may look the same but the x value has become a negative because the angle is in the left side (negative side) of the graph but the y value stays the same because it is still in the positive side of the graph. In the third quadrant, there is a 225* with the reference angle of 45* that is similar to the 45* in the first quadrant. However, like the 30*, even though the reference is the same, the angle, radians, and ordered pairs are completely different from the 45* in the first quadrant. As for the 300* in the fourth quadrant, the reference angle is 60* like the first quadrant but the 300*, the radian, and the ordered pair specified in the fourth quadrant are completely different from the 60* in the first quadrant. This is also seen when the angles with the same reference angle are drawn in all the quadrants and connecting them would make a quadrilateral in the unit circle. The values for each point on the unit circle are identical except for the (+-) which is determined by where the point is on the graph. With this, it helps determine the rest of the unit circle and its values just by using the first quadrant and the 3 special right triangles. 


Inquiry Activity Reflection

The coolest thing I learned from this activity was a single angle can have an infinite possibility of coterminal angles. 

This activity will help me in this unit because all the concepts revolve around knowing the unit circle and the special properties of the angles in the unit circle. The concepts that are most important in relation to the unit circle are 7,8,9. 

Something I never realized about special right triangles and the unit circle is how the special right triangle shows up in the unit circle and plays a significant role in filling out the rest of the unit circle and how the unit circle actually has a method for completing it when I all did last year was try to memorize everything. 

RWA 1 Unit M Concept 4 - Conic Sections in Real Life

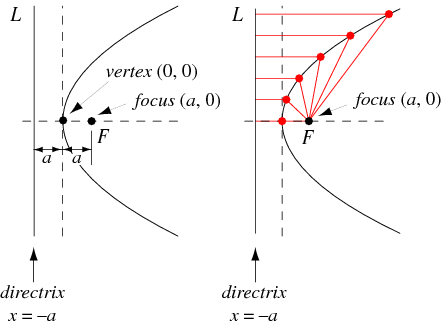
1. Parabola - "Set of all points that are equal distance from focus and directrix."
2. Algebraically (x-h)^2=4p(y-k) & (y-k)^2=4p(x-h)
    Graphically -

Image Cite

             The formula used for parabola is unique from the other conic sections because it only has term that is squared while the rest are not. As for the graph, it is unique in having one arc with points of all equal distance between the foci and directrix.

             Writing standard form - Decided whether the graph is x^2 or y^2, move the squared term and its like terms to one side and the others to the rest, complete the square correctly and make sure that the side that does not have the squared term is not negative. If it is take, take out the negative. 

             Graphing parabola - Standard form, plot vertex, plot the focus and directrix "p" units away from vertex, sketch axis of symmetry, sketch parabola. 

             "Eccentricity is how much a conic section deviates from being circular." For parabolas, the eccentricity should always equal to 1 or else you did something wrong. To determine the eccentricity of a parabola, you use the formula e=c/a. Your c & a are found by the standard form of the parabola. The foci is the distance from the center to the interior that gives the parabola its shape. The directrix is the line at the exterior of the parabola that is also the equal distance from the center. The foci and directrix determine if the graph is wide or thin because the points are all equal distance from the foci and directrix.

               Always make sure your formula is in standard form as well when graphing parabolas because it greatly helps for determining the required parts for the graph. Depending if P is positive and if the equation is x or y, will tell the person how the parabola will be graph. Ex. P is positive and the equation is x^2 means the parabola will open up. 

             After graphing parabola go through the checklist so that you can get full credit on your problem and not make any mistakes. Also make sure that the foci is inside the parabola while the directrix is outside of the parabola. Labeling each part is important so that you do not get messed up somehow.

3.          A real world use of parabolas are the parabolic skis. The skis make it much easier to turn and the turning area to help make a perfect arc with less skill. This skis are the improved versions of the original circular cut skis. Compared to the original skis, the original tend to only move in a straight line making it much harder and requiring more energy to make sharp turns. 

            These skis are more commonly used now because they provide more efficiency and require less energy. By forming perfect arcs and increasing the speed of the turns, the skiers are able to use little energy and save time on their runs for better times. Also, the parabolic skis offer more control which is essential for controlling the skis to be more efficient.  Parabolic Skis

            Here is a video to help people understand how the shape of the skis affect the riders and their times in their races and marathons. 

4. Citations
    Image
     Example
     Video

WPP 10 Probability in Various Situations

Create your own Playlist on LessonPaths!

Hey there, things to look out for when you look at my blog is that the the situation where the problem occurs greatly affects the how to set up the problem like for problem 12 is mutually exclusive and problem 13 is non mutually exclusive. Reading the problem carefully is very important because using the wrong method to solve will end up with the wrong answer. Thank you!