2. Algebraically (x-h)^2=4p(y-k) & (y-k)^2=4p(x-h)
Graphically -
The formula used for parabola is unique from the other conic sections because it only has term that is squared while the rest are not. As for the graph, it is unique in having one arc with points of all equal distance between the foci and directrix.
Writing standard form - Decided whether the graph is x^2 or y^2, move the squared term and its like terms to one side and the others to the rest, complete the square correctly and make sure that the side that does not have the squared term is not negative. If it is take, take out the negative.
Graphing parabola - Standard form, plot vertex, plot the focus and directrix "p" units away from vertex, sketch axis of symmetry, sketch parabola.
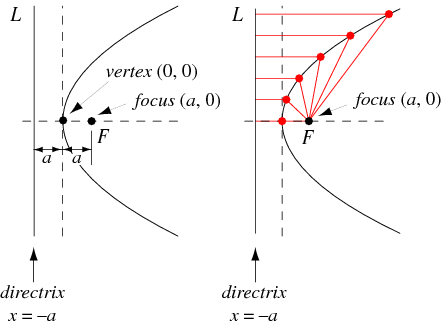
"Eccentricity is how much a conic section deviates from being circular." For parabolas, the eccentricity should always equal to 1 or else you did something wrong. To determine the eccentricity of a parabola, you use the formula e=c/a. Your c & a are found by the standard form of the parabola. The foci is the distance from the center to the interior that gives the parabola its shape. The directrix is the line at the exterior of the parabola that is also the equal distance from the center. The foci and directrix determine if the graph is wide or thin because the points are all equal distance from the foci and directrix.
Always make sure your formula is in standard form as well when graphing parabolas because it greatly helps for determining the required parts for the graph. Depending if P is positive and if the equation is x or y, will tell the person how the parabola will be graph. Ex. P is positive and the equation is x^2 means the parabola will open up.
After graphing parabola go through the checklist so that you can get full credit on your problem and not make any mistakes. Also make sure that the foci is inside the parabola while the directrix is outside of the parabola. Labeling each part is important so that you do not get messed up somehow.
3. A real world use of parabolas are the parabolic skis. The skis make it much easier to turn and the turning area to help make a perfect arc with less skill. This skis are the improved versions of the original circular cut skis. Compared to the original skis, the original tend to only move in a straight line making it much harder and requiring more energy to make sharp turns.
These skis are more commonly used now because they provide more efficiency and require less energy. By forming perfect arcs and increasing the speed of the turns, the skiers are able to use little energy and save time on their runs for better times. Also, the parabolic skis offer more control which is essential for controlling the skis to be more efficient. Parabolic Skis
Here is a video to help people understand how the shape of the skis affect the riders and their times in their races and marathons.
4. Citations
Image
Example
Video
No comments:
Post a Comment